Calculating the derivative of a tag
Searching for periods when parameter readings exhibit increases or decreases can be highly valuable, as variations often signal potential process issues. By calculating the derivative, you can assess a process's responsiveness to changes in specific parameters.
Tip
For noisy or fluctuating signals, it is useful to smooth the trend with an average aggregation before calculating the derivative to obtain the closest approximation to the derivative of a chosen function.
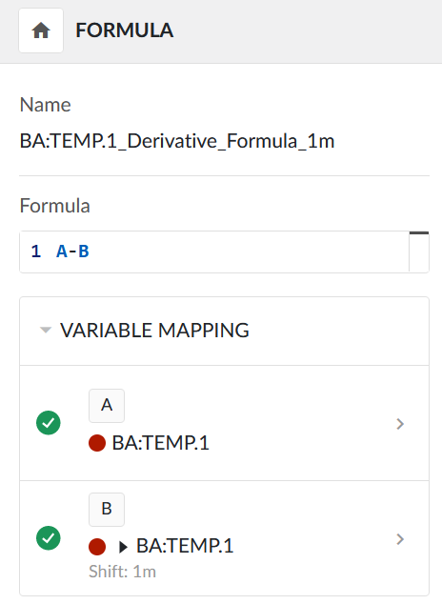
Calculate the slope of the tag using a Tag Builder Formula [https://userguide.trendminer.com/en/77754-tag-builder--formula.html]. The tag is subtracted from a time-shifted version of itself, and this subtraction occurs over a short interval of time. The accuracy of the approximation to the true derivative improves as the duration of this interval decreases.
Formula:
A - B
Variable mapping:
A = (Smoothed) tag with desired derivative to be calculated.
B = (Smoothed) tag with desired derivative to be calculated, shifted by e.g., 1 minute.
Creating the derivative by using a formula has several advantages:
It's highly accurate for short time intervals (delta_t & 2x index resolution).
Ideal for extended trends, such as fouling detection, when delta_t exceeds 24 hours.
Allows unit calculations within the formula.
Simplifies nested formulas by counting as just one level when calculating slopes.
 | 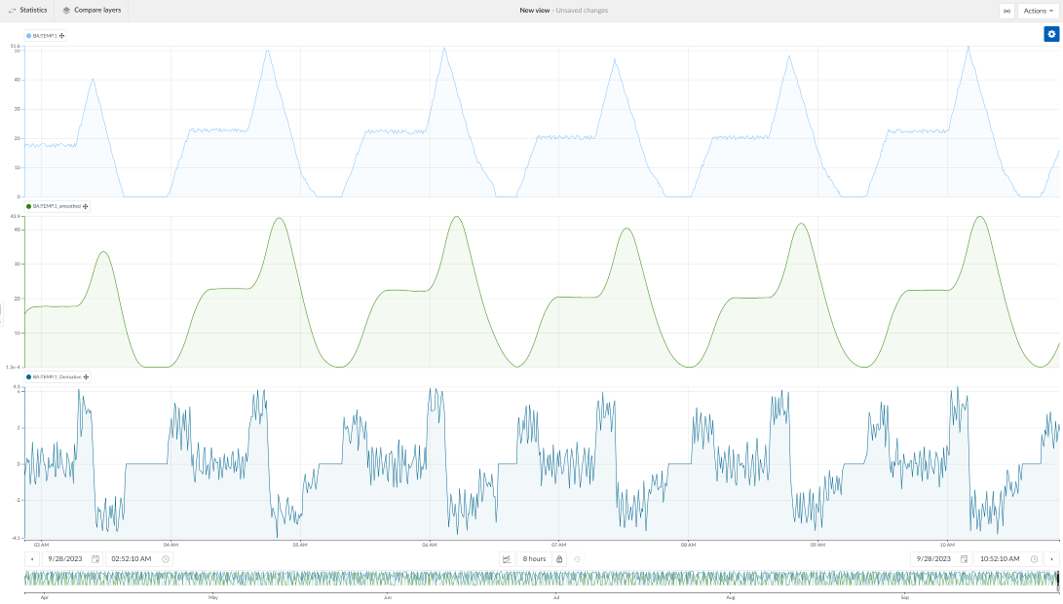 |
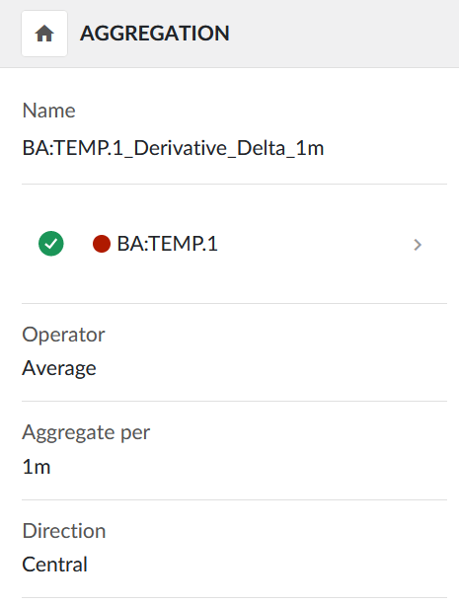
The derivative can be simplified by using a delta aggregation.
Tag to aggregate: (Smoothed) tag with desired derivative to be calculated
Operator: Delta
Direction: e.g., Central
Aggregate per e.g., 1 minute
 | 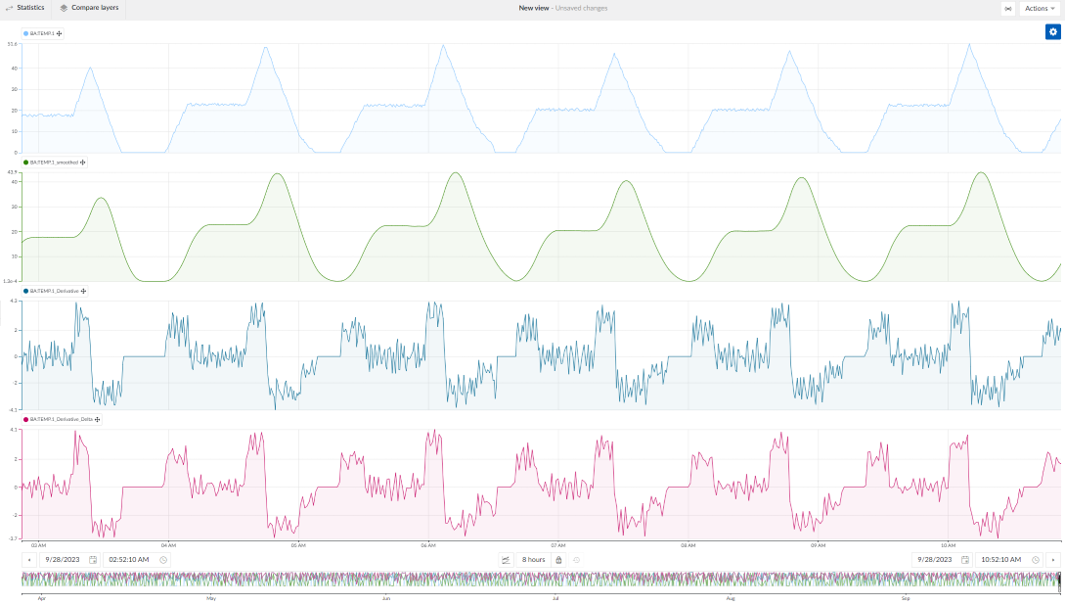 |