Calcul de la dérivée d'un Tag
La recherche de périodes au cours desquelles les relevés de paramètres présentent des augmentations ou des diminutions peut s'avérer très utile, car les variations signalent souvent des problèmes potentiels au niveau du processus. En calculant la dérivée, vous pouvez évaluer la réactivité d'un processus aux changements de paramètres spécifiques.
Astuce
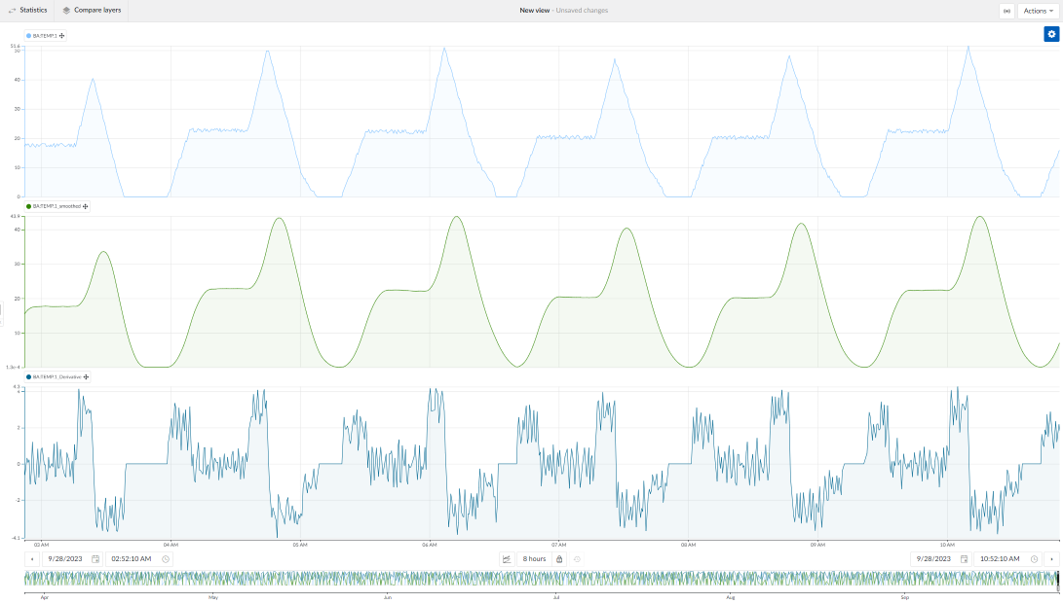
Pour les signaux bruyants ou fluctuants, il est utile de lisser la tendance avec une agrégation moyenne avant de calculer la dérivée pour obtenir l'approximation la plus proche de la dérivée d'une fonction choisie.
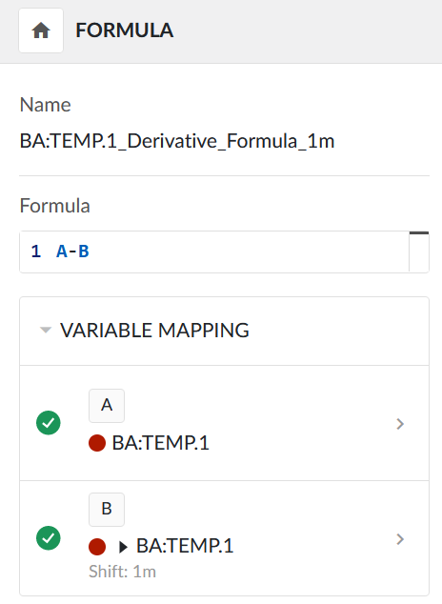
Calculez la pente de la balise à l'aide d'un Formule de création de balises. Le Tag est soustrait d'une version décalée dans le temps de lui-même, et cette soustraction se produit sur un court intervalle de temps. La précision de l'approximation de la vraie dérivée s'améliore à mesure que la durée de cet intervalle diminue.
Formule:
A - B
Cartographie variable :
A = Tag (lissé) avec la dérivée souhaitée à calculer.
B = Tag (lissé) avec la dérivée souhaitée à calculer, décalée de 1 minute par exemple.
La création de la dérivée à l'aide d'une formule présente plusieurs avantages :
Il est très précis pour les intervalles de temps courts (delta_t & résolution de l'indice 2x).
Idéal pour les tendances prolongées, telles que la détection de l'encrassement, lorsque le delta_t dépasse 24 heures.
Permet d'effectuer des calculs d'unités dans la formule.
Simplifie les formules imbriquées en ne comptant qu'un seul niveau dans le calcul des pentes.
 |  |
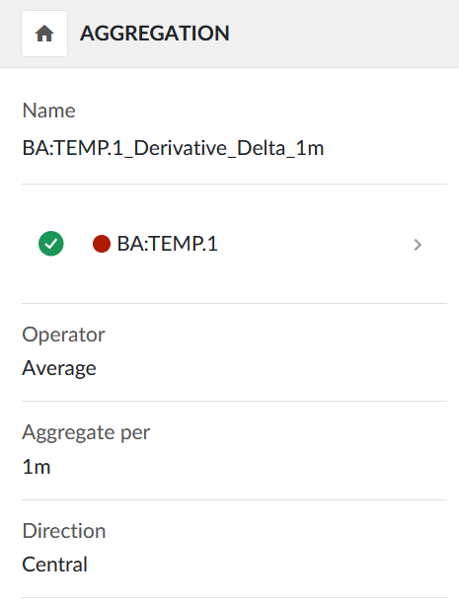
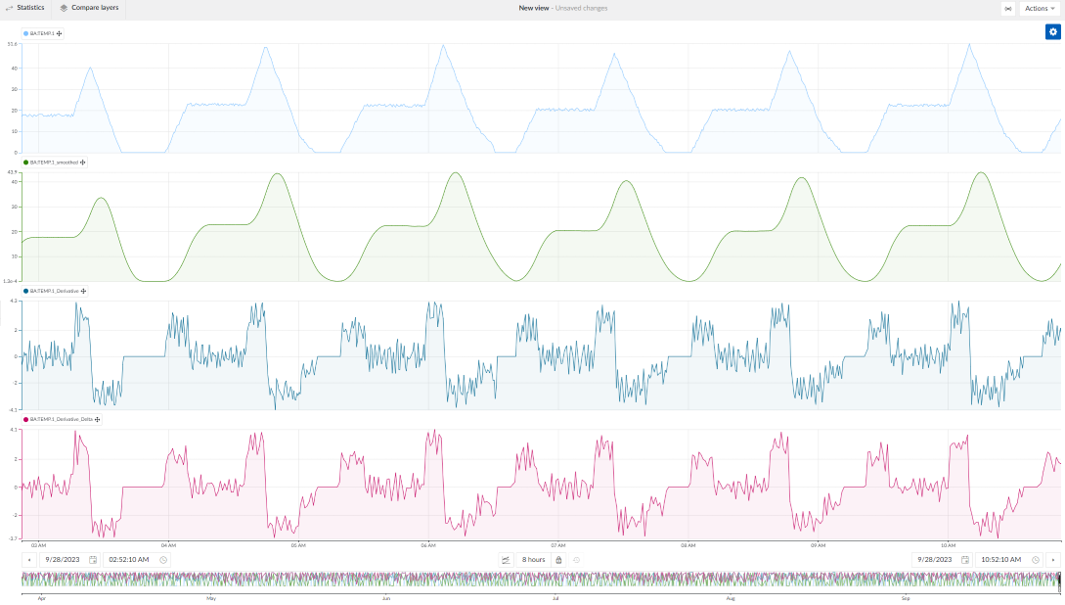
La dérivée peut être simplifiée en utilisant une agrégation delta.
Tag à agréger : Tag (lissé) avec la dérivée souhaitée à calculer
Opérateur : Delta
Direction : par exemple, centrale
Agrégat par exemple, 1 minute
 |  |